[LeetCode] 530. Minimum Absolute Difference in BST - Java

Minimum Absolute Difference in BST - LeetCode

 

문제

 

Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.

 

Example 1:

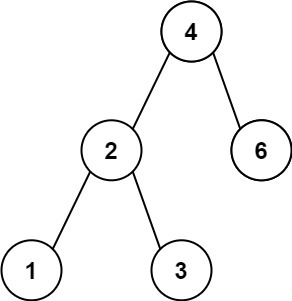
Input: root = [4,2,6,1,3]
Output: 1

Example 2:

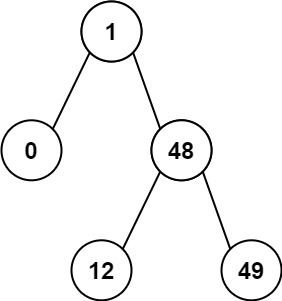
Input: root = [1,0,48,null,null,12,49]
Output: 1

 

Constraints:

• The number of nodes in the tree is in the range [2, 104].
• 0 <= Node.val <= 105

 

BST(이진탐색트리)의 root노드가 주어졌을 때, 트리를 모두 순회해서 서로 다른 두 노드 값들 사이의 절대값 차의 최소값을 반환하는 문제이다.

 

---

 

내 풀이

 

BST의 중위순회 (In-order Traversal)

          A
       /     \
      B       C
     / \     / \
    D   E   F   G

중위순회는 순회의 순서가 다음과 같다

💡 왼쪽 서브트리 → 현재 노드 → 오른쪽 서브트리

따라서 루트노드부터 시작했을 때,

1. 왼쪽 서브트리 방문 : D, B, E
2. 현재 노드 : A
3. 오른쪽 서브트리 방문 : F ,C, G

중위 순회의 결과는 D, B, E, A, F, C, G이다.

중위 순회는 BST에서 노드들을 오름차순으로 방문하는 순서이다.

여기서 왼쪽과 오른쪽의 순서를 바꾸면 내림차순으로 방문 가능하다.

 

 

코드

문제는 각 노드 값들의 절대값 차의 최소를 구하는 문제이다.

각 노드들을 방문하여 값들을 모두 저장한 다음, 정렬하고, 모든 값들의 절대값 차를 구하고, 그 중 최소를 반환할 수도 있지만 시간, 공간 복잡도 상 비효율적인 방법일 수 있다.

 

이미 정렬된 구조를 가지고 있는 이진탐색트리에서는 중위순회를 통해 노드들을 오름차순으로 방문할 수 있고,

별다른 추가 연산 없이 노드 방문과 동시에 최소 절대값 차를 계속 업데이트 할 수 있다.

 

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int minValue = Integer.MAX_VALUE;
    int preValue = -1;

    public int getMinimumDifference(TreeNode root) {
        inorder(root);
        return minValue;
    }

    public void inorder(TreeNode now){
        if(now== null) return;

        inorder(now.left);

        if(preValue != -1){
            minValue = Math.min(minValue, Math.abs(preValue - now.val));
        }
        preValue = now.val;

        inorder(now.right);
    }
}

inorder 메서드 안에 중위순회 로직을 구현했다.

문제에서 노드 값의 범위가 0 <= Node.val <= 10^5 이기 때문에 이전노드의 값을 저장하는 preValue 변수의 초기값은 -1로 설정하고,

preValue 가 -1이 아닐때만 이전노드와 현재노드 값의 절대값 차를 계산하고 업데이트한다.

 

• 시간복잡도 : O(n)  - 트리 순회
• 공간복잡도 : O(logn)
  • 중위 순회 메서드는 재귀적으로 호출되기 때문에 호출 스택(call stack)을 사용하여 함수 호출 및 복귀 정보를 저장한다.
  • 재귀 호출의 깊이는 트리의 높이(h)와 관련되어 있으며, 최악의 경우 트리의 높이와 같다.
  • 트리의 높이 h는 logn에 가깝다 (n = 노드의 개수)
  • 현재 코드에서는 모든 노드를 방문하기 때문에 재귀 호출 스택의 공간 복잡도는 최악의 경우 트리의 높이(h=logn)에 비례하여 O(logn)이다.